Screening Normalization

To normalize a screen we rely on a number of normalisations. The first normalization step involves the inter-plate variance. Here we normalize the different biological replicas for each plate. The second step normalizes the differences between the different plates. This is called the inter-plate variance normalization.

Plates: 001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041

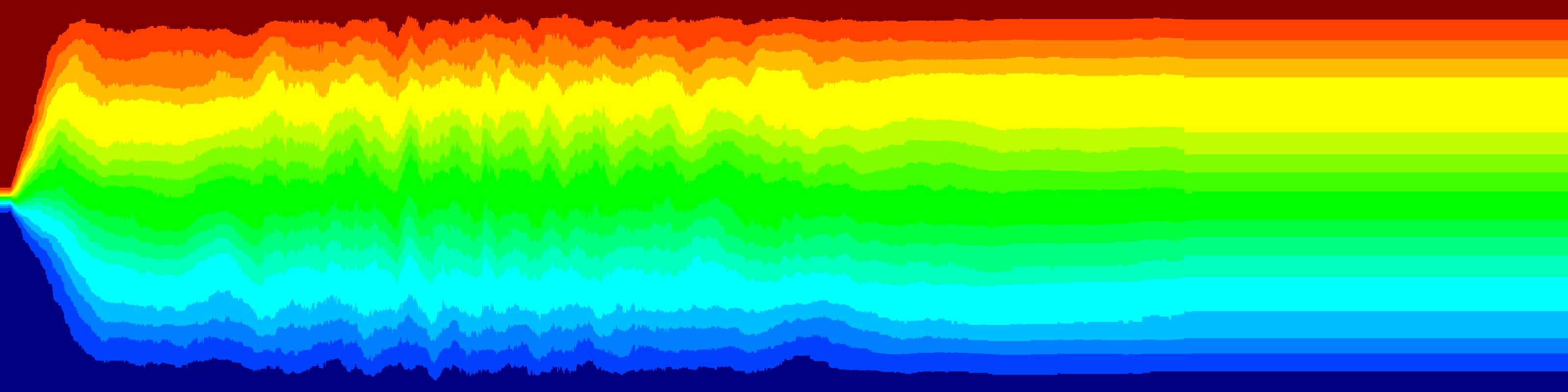
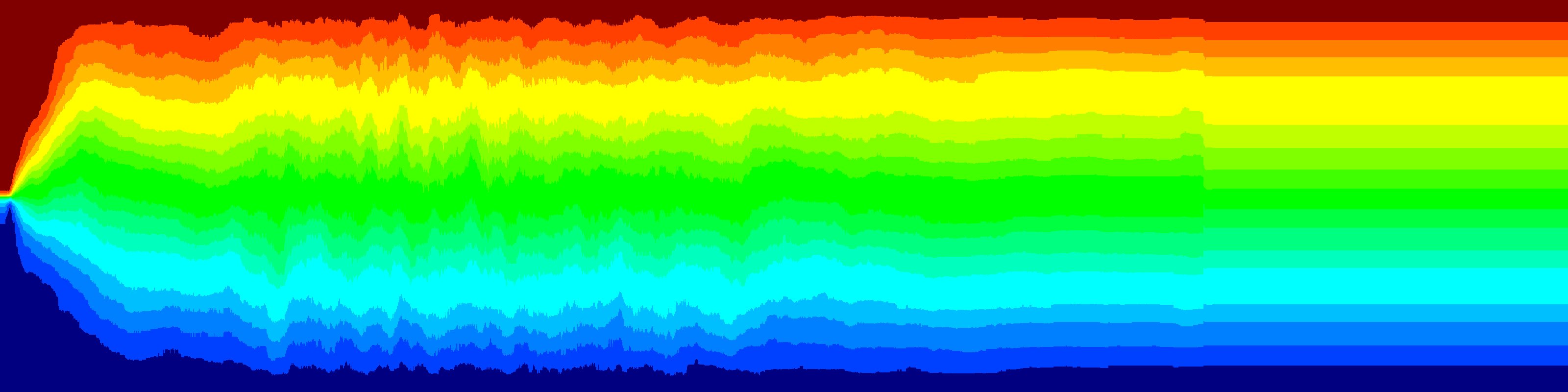
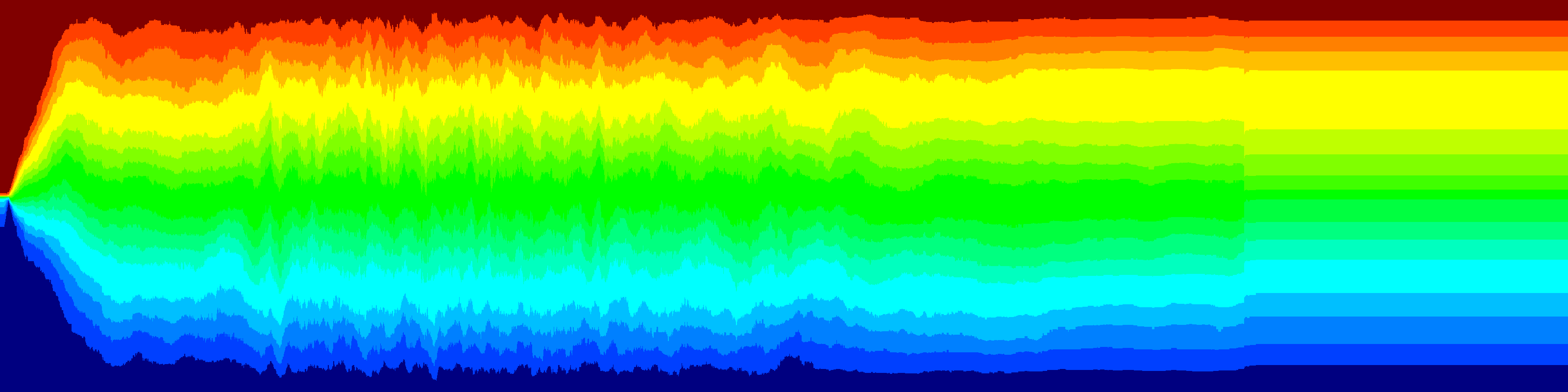
The variance between the renila and firefly colors is shown below. The 41 lines are the different plates. Each plate is represented as the average histogram on that plate.

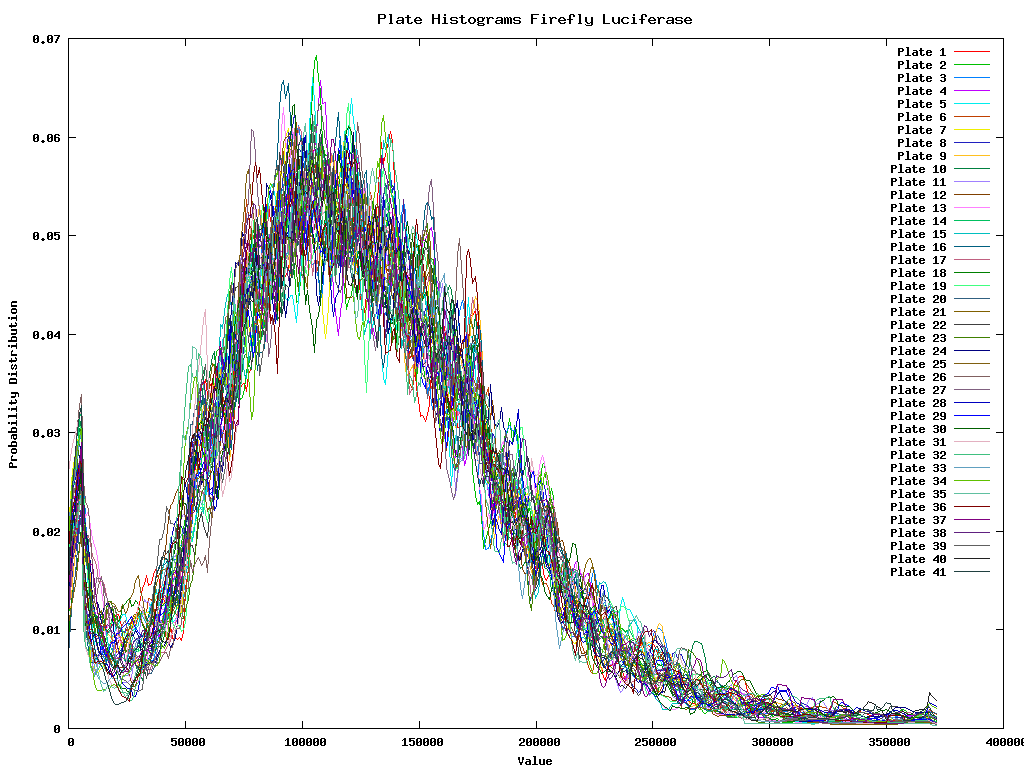
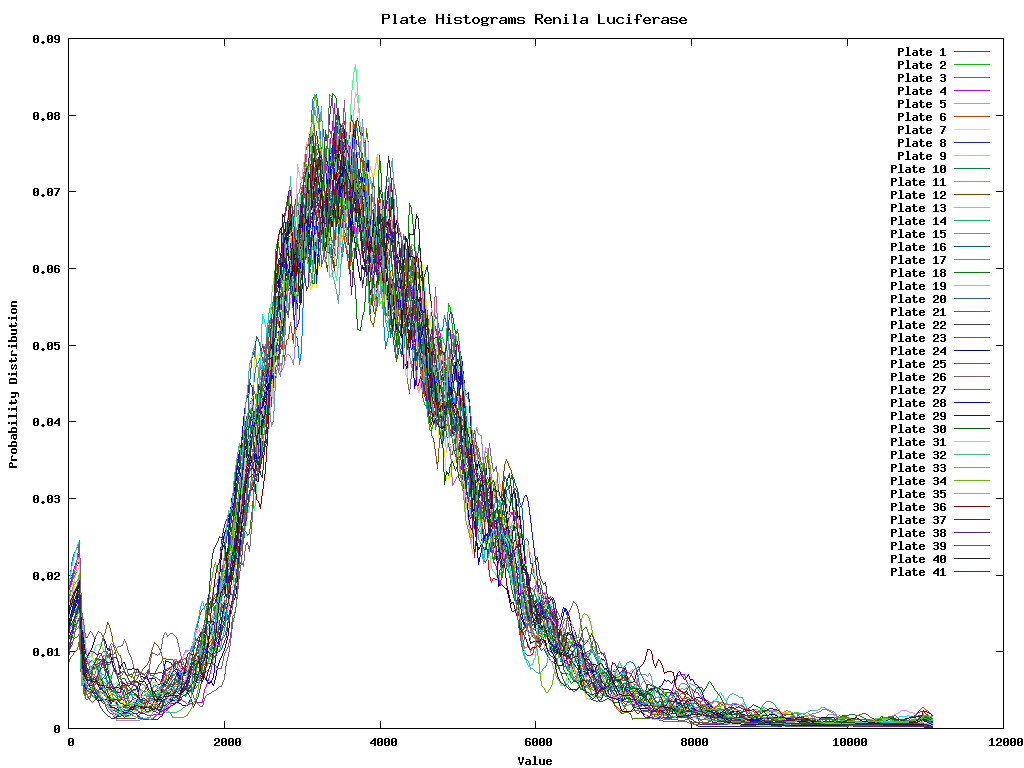
Because the firefly luciferase reflects the number of viable cells we must divide the renila intensity by the firefly intensity for each well. Once this is done we are interested in the outliers of the data, or those that are sufficiently different from the mean (a couple of standard deviations). So for each of the two colors we develop first a intensity dependent error distribution. This distribution could then be used to have a confidence interval with each measurement. It does however not solve the problem of measuring the mean of the ratios. As such it is better to first ensure that the ratio between the two colors will be 1 for the gross of the data. Therefore we need to perform the inter-color normalization before we calculate the ratios.

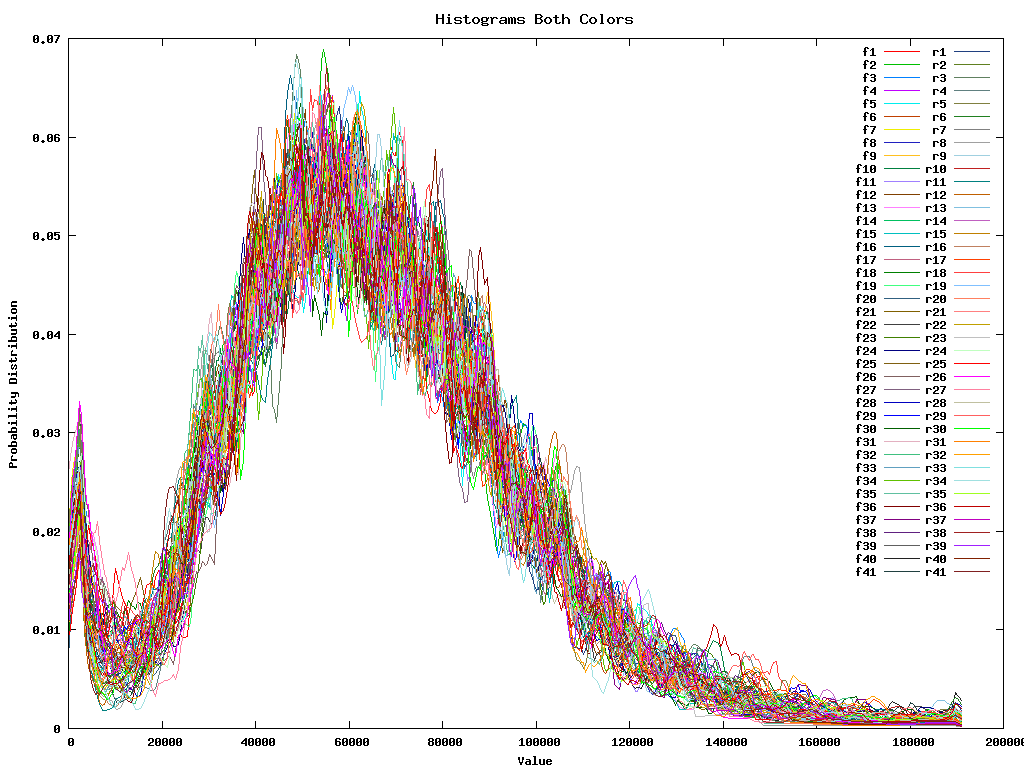
Of course all these different steps are essentially not necessary since we can as well take all 4 replicas of all 41 plates for the two colors and immediatelly normalize them all at the same time. This gives:

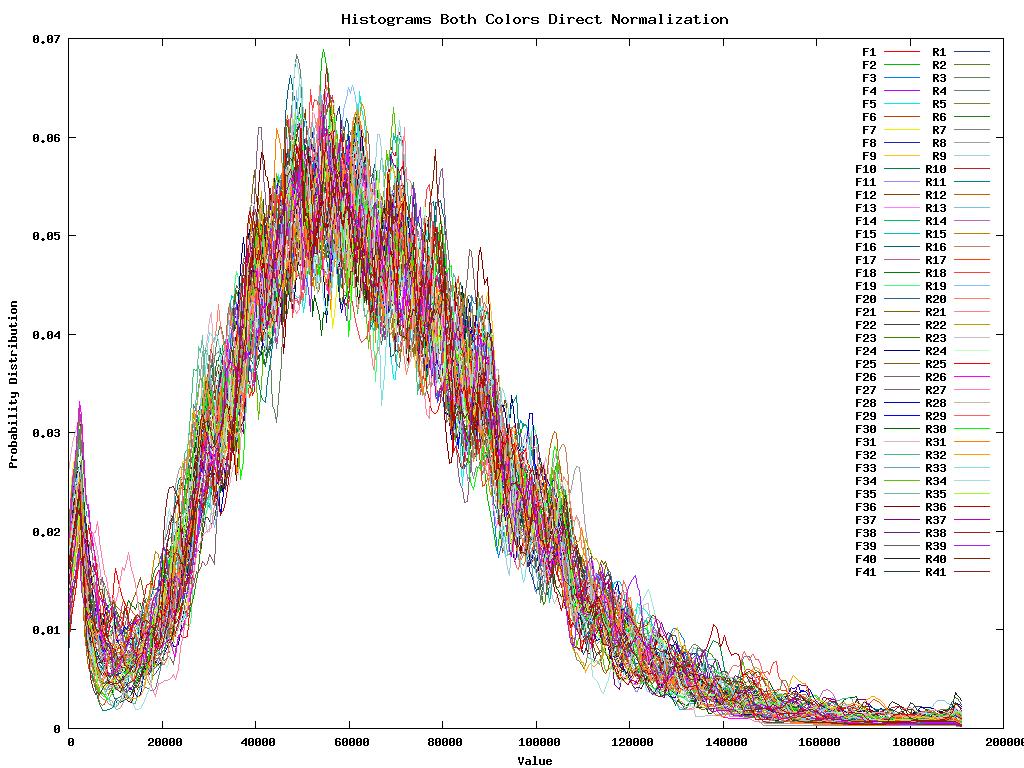
Once these normalizations have taken place we are interested in setting out an intensity dependent confidence interval. This can be individually calculated for F, R or for all samples. Since they are fairly similar we continue working with the tottal intensity dependent confidence interval.